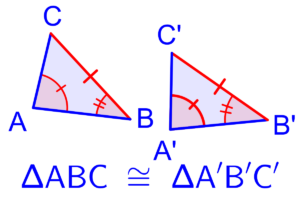
Demystifying SAS: Unlocking the Secrets of Triangle Congruence
In the realm of geometry, proving triangles congruent (having all corresponding sides and angles equal) can be a crucial skill. The Side-Angle-Side (SAS) congruence rule is a powerful tool for establishing this equivalence. This article delves into the intricacies of SAS, exploring the conditions under which it guarantees congruent triangles and providing clear examples and explanations.
Understanding Triangles and Congruence:
- Triangles: Basic building blocks of geometry, triangles are three-sided polygons with three interior angles that always add up to 180 degrees.
- Congruence: Two triangles are considered congruent if their corresponding sides and angles are equal. This means if you place one triangle on top of the other, they would perfectly overlap.
The Power of SAS:
The SAS congruence rule states that if two triangles have:
- Two Sides Congruent: Two corresponding sides of the triangles must be equal in length.
- The Included Angle Congruent: The angle formed between the two congruent sides in each triangle must also be equal in measure.
Then, the two triangles can be proven congruent.
Visualizing SAS:
Imagine two triangles, Triangle ABC and Triangle DEF. If we know that:
- Side AB of Triangle ABC is equal in length to Side DE of Triangle DEF (AB = DE)
- Side AC of Triangle ABC is equal in length to Side DF of Triangle DEF (AC = DF)
- Angle B at the vertex where the two congruent sides meet in Triangle ABC is equal in measure to Angle E at the vertex where the two congruent sides meet in Triangle DEF (∠B = ∠E)
Based on the SAS rule, we can definitively say that Triangle ABC is congruent to Triangle DEF (ΔABC ≅ ΔDEF).
Why Does SAS Work?
The underlying principle behind SAS lies in the unique relationship between sides and angles in a triangle. The included angle is “sandwiched” between the two congruent sides. This specific configuration dictates the shape and size of the triangle. If two triangles share two sides and the included angle, their overall shape and size must be identical, making them congruent.
Exploring the Logic:
Imagine constructing a rigid triangle model out of metal rods. If you fix two rods of equal length (representing the congruent sides) at a specific angle, the resulting triangle shape is predetermined. Any other triangle formed with those same two rod lengths connected by the same angle will be identical. This illustrates the concept behind the SAS rule.
Limitations of SAS:
It’s important to note that SAS doesn’t guarantee congruence in every scenario. Here are some key limitations:
- SSS (Side-Side-Side) Not Sufficient: Just having two sides of each triangle congruent and the third sides not specified is not enough to ensure congruence. Imagine two triangles with two sides of equal length but different third side lengths. They could be different shapes entirely.
- AAS (Angle-Angle-Side) Not Always Applicable: While there’s an Angle-Angle-Side (AAS) congruence rule under specific conditions, it’s not as broadly applicable as SAS.
Applying SAS in Action:
Let’s look at some practical examples of how to use SAS to prove triangle congruence:
Example 1:
- Given: Triangle ABC with AB = 8 cm, AC = 10 cm, and ∠B = 50°
- Given: Triangle DEF with DE = 8 cm, DF = 10 cm, and ∠E = 50°
Since both triangles have two sides (AB and AC; DE and DF) and the included angle (∠B and ∠E) equal in measure, we can use SAS to conclude that Triangle ABC is congruent to Triangle DEF (ΔABC ≅ ΔDEF).
Example 2:
- Given: Triangle PQR with PQ = 12 cm, PR = 7 cm, and ∠Q = 45°
- Given: Triangle XYZ with XY = 12 cm, YZ = 7 cm, and ∠Y = 45°
Here, both triangles share two sides (PQ and PR; XY and YZ) with the same length. However, we don’t have information about the included angles (∠Q and ∠Y). Based solely on side lengths, we cannot use SAS to prove congruence.
Beyond the Basics:
The SAS rule forms the foundation for other triangle congruence theorems, such as the HL (Hypotenuse-Leg) congruence rule applicable to right triangles. By mastering SAS, you can unlock various techniques for proving triangle congruence in different scenarios.
FAQs:
1. Can I use SAS if only one side and the included angle are congruent?
No, SAS requires two sides to be congruent. If only one side and the included angle are equal in two triangles, it’s not enough to guarantee congruence. There might be other triangles that share those characteristics but have different overall shapes and sizes.
2. What if two triangles have all three sides congruent? Does that guarantee congruence?
Yes! Having all three corresponding sides of two triangles equal in length falls under the SSS (Side-Side-Side) congruence rule. This rule states that if all three sides of one triangle are congruent to the corresponding sides of another triangle, then the two triangles are guaranteed to be congruent.
3. Is there a way to prove congruence if two triangles have two angles congruent?
There’s a specific case where two congruent angles and a side between them can establish congruence. This is known as the AAS (Angle-Angle-Side) congruence rule. However, unlike SAS, AAS has a crucial additional requirement:
- The non-included angles must be opposite the congruent side. In simpler terms, the two congruent angles must not share a common vertex (corner point) in the triangle.
4. Where can I find more information about triangle congruence?
Here are some informative resources for further exploration:
- Khan Academy: https://www.khanacademy.org/math/geometry-home/triangle-properties (This website offers interactive lessons and practice problems on triangle congruence)
- National Library of Virtual Manipulatives: http://nlvm.usu.edu/ (This website provides interactive tools for visualizing and manipulating triangles)
- Geometry Reference: https://en.wikipedia.org/wiki/Congruence_%28geometry%29 (The Wikipedia page on congruent triangles offers a comprehensive overview of the various congruence rules, including SAS)
The Takeaway:
Understanding SAS empowers you to confidently prove triangle congruence in numerous situations. By recognizing the limitations of SAS and exploring other congruence rules, you can expand your geometric problem-solving skills. Remember, practice and exploration are key to mastering these concepts. So, grab a compass, ruler, and some paper, and start drawing triangles!